Author: B J Wernick PrEng BScEng
Date: 22 March, 2007
Recently, a colleague emailed me from Dubai to discuss water flow in a district cooling system with nominal pipe sizes up to 1700mm in diameter. I can actually walk upright in a pipe this size!
The question is, what is the most reliable way to calculate the pressure drop in a pipe of this bore. You must realize that this is not your average 150mm diameter chilled water pipe at the local shopping center where you can pull the impeller out of the pump, have it trimmed and back the next day. Make a mistake here and you could end up, as my colleague puts it, "with a nice quiet retirement plan - Dubai jail".
I looked in the ASHRAE Handbook and various other references and find that the biggest diameter in the ASHRAE quick selection chart is 600mm. This means that we must go back to the theory to find a solution.
The most common way of expressing the pressure drop of a piped fluid is to use the D'Arcy-Weisbach equation.
| dP = ½ ρ ƒ L V2 / D | (1) | |
|
where dP = Frictional pressure drop, Pa ρ = Fluid density, kg/m3 ƒ = Friction factor, dimensionless V = Fluid velocity, m/s D = Inside diameter, m L = Pipe length, m |
||
The only unknown here is the friction factor (f).
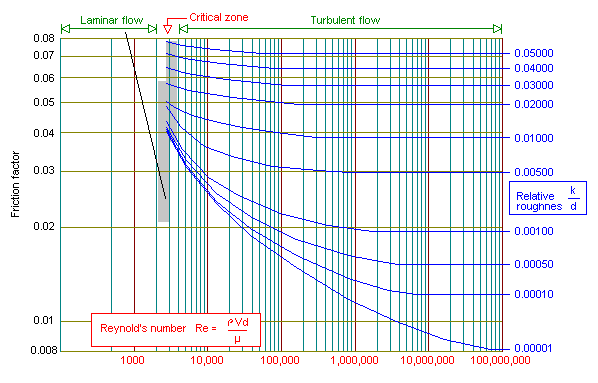
The friction factor is based on the pioneering work of Thomas Stanton (1865-1931) who with J. R. Pannel conducted experiments on a number of pipes of various diameters, materials and fluids. At the time, the plot of this data was therefore sometimes known as the Stanton diagram. A German engineer Johann Nikuradse (1894) extended the results by doing experiments on artificially roughened circular pipes. An American engineer Lewis F Moody (1880-1953) prepared the diagram shown in figure 1 for use with ordinary commercial pipes. Today, the Moody diagram is still widely used and is the best means available for estimating the friction factor.

Figure 1. Moody Diagram
The flow parameter is a dimensionless number called the Reynolds Number.
| Re = ρ V D / μ | (2) | |
|
where V = Fluid velocity, m/s D = Inside diameter, m μ = Dynamic viscosity of the fluid, μPa·s |
||
The various curves on the Moody diagram are relative roughness where (k) is the absolute roughness in mm. This pipe roughness is well documented for different types of pipes as seen in Table 1.
| Material | Roughness, mm |
|---|---|
| Riveted steel | 0.9 - 9.0 |
| Concrete | 0.3 - 3.0 |
| Cast Iron | 0.26 |
| Sheet metal | 0.15 |
| Commercial steel | 0.046 |
| Drawn tube | 0.0015 |
Ref: Hodge
The problem with the Moody diagram is that it is not suitable for automatic processing. The answer is therefore to find some sort of relationship between the variables. This was done by Colebrook in 1939 where he presented the following implicit relationship.
| 1/√f = -2 Log10(e/(3.7D) + 2.51/(Re √f)) | (3) | |
|
where Re = Reynolds number, dimensionless D = Inside diameter, m e = Roughness, m |
||
Note: This equation is shown in different forms in the various references.
Nothing is ever that simple. In order to solve equation (3) you need to know the friction factor but as it turns out, with a reasonable starting guess and a few successive substitutions, it converges fairly quickly.
Before the wide-spread use of computers however, this iterative process was not practical so Hazen and Williams suggested the following relationship.
| dP = K Qn | (4) | |
|
where Q = Flow rate, m3/s K and n are experimentally determined coefficients |
||
K and n are determined by curve fitting the data from the Moody diagram. For turbulent piped water flow the Hazen-Williams equation becomes
| dP = 102.5 L (Q/C)1.852 / D4.8704 | (5) | |
|
where C = Hazen-Williams coefficient Q = Flow rate, m3/s D = Inside diameter, m |
||
The Hazen-Williams coefficient (C) is a dimensionless number indicative of the pipe roughness and has the following approximate values.
| Type of Pipe | C |
|---|---|
| Extremely smooth and straight | 140 |
| New, smooth cast iron | 130 |
| Average cast iron, new riveted steel | 110 |
| Vitrified sewer pipes | 110 |
| Cast iron, some years service | 100 |
| Cast iron, in bad condition | 80 |
Ref: Hodge
The problem with the Hazen-Williams formulation is that it is based on a specified fluid with a fixed temperature. Also, the coefficient C does not allow for the change in relative roughness with diameter. The best way to illustrate the validity of the Hazen-Williams equation is by example.
Example 1.
Find the pressure rate of water in a 1700mm diameter steel pipe with a velocity of 1 m/s at 20°C and 80°C.
| t, °C | Viscosity, mPa·s | Density, kg/m3 |
|---|---|---|
| 20 | 1.008 | 998.21 |
| 80 | 0.358 | 971.63 |
Ref: Stoecker and Jones
Calculate the results with the D'Arcy Weisbach equation.
| Value | 20°C | 80°C |
|---|---|---|
| Reynolds Number | 1.696 x 106 | 4.719 x 106 |
| Friction factor | 0.01144 | 0.0104 |
| Pressure Rate, kPa/m | 0.003357 | 0.002972 |
Note: The values in this table were calculated using the TechniSolve Water program.
We now compare these with the Hazen-Williams equation with C=130
dP/L = 102.5 (2.2698/130)1.852 / 1.74.8704 = 0.0043 kPa/m
Why the big difference (almost 50% higher)? The reason is that I chose the Hazen-Williams coefficient from a text book and it does not necessarily agree with the surface roughness of 0.046mm. Notice also that Hazen-Williams cannot compensate for the temperature change since a particular set of values have been used in the original correlation.
If we choose C=140 (extremely smooth and straight) dP/L= 0.0037 kPa/m. The relative roughness of large bore pipes would be small so it would make sense that the pipe is extremely smooth. But this doesn't make things better, all we are doing now is guessing numbers to fit with D'Arcy.
Example 2
Example 1 above was selected to highlight problems with the Hazen-Williams formulation. We can confirm our suspicion that for small bore pipes, the Hazen-Williams formulation is reasonable. Calculate the pressure rate on a 65mm bore pipe with a velocity of 2m/s (6.637 l/s) at 20°C. (Use C=130)
dP (D'Arcy-Weisbach) = 0.6314 kPa/m
dP (Hazen-Williams) = 0.6976 kPa/m (10% higher than D'Arcy)
Since the Hazen-Williams equation is based on a curve-fit to the Moody diagram, I can see no reason for not using Moody directly. The Hazen-Williams is clearly a simplification to reduce the manual computation of the friction factor.
When selecting a pipe diameter from the traditional quick selection chart, it was customary to limit the pressure rate to 1 kPa/m and also not to exceed 3m/s. This seems to work fine if the pipe diameter is less than 300mm. At big diameters, this 3 m/s limit would result in very low pressure rates as seen in the example 1. It would probably make more sense to settle on a lower pressure rate of say 0.1 kPa/m for large bore pipes.
SAIRAC 2004 Technical Data Manual, Wernick B.J. Ed.
Hodge, B.K. "Analysis and Design of Energy Systems", Prentice-Hall Inc. 1985.
ASHRAE 1993 Fundamentals Handbook, Pipe Sizing Chapter 33, pp 33.5
Colebrook, C.F. "Turbulent flow in pipes with particular reference to the transition region between smooth and rough pipe", Journal of Civil Engineering, v 12, no 4, pages 1330156, February 1939.
Stoecker, W.F. and Jones, J.W. "Refrigeration & Air Conditioning", 2nd Ed. McGraw Hill 1982.
Massey, B.S. "Mechanics of Fluids", 4th Ed. Von Nostrand Reinhold, 1979.
Moody, L.F. "Friction factors for pipe flow", Transactions of the American Society of Mechanical Engineers, Vol 66 671-684 (1944).
Copyright TechniSolve Software © 2004 All rights reserved
For more information and software, visit the web site